Dt=1/2Fm ,
(2)
где Fm - максимальная частота спектра преобразуемого сигнала. При этом выражение (1) переходит в известное выражение теоремы отсчетов
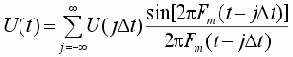 |
(3) |
Для сигналов со строго ограниченным спектром это выражение является тождеством. Однако спектры реальных сигналов стремятся к нулю лишь асимптотически. Применение равномерной дискретизации к таким сигналам приводит к возникновению в системах обработки информации специфических высокочастотных искажений, обусловленных выборкой. Для уменьшения этих искажений необходимо либо увеличивать частоту дискретизации, либо использовать перед АЦП дополнительный фильтр нижних частот, ограничивающий спектр исходного сигнала перед его аналого-цифровым преобразованием.
В общем случае выбор частоты дискретизации будет зависеть также от используемого в (1) вида функции fj(t) и допустимого уровня погрешностей, возникающих при восстановлении исходного сигнала по его отсчетам. Все это следует принимать во внимание при выборе частоты дискретизации, которая определяет требуемое быстродействие АЦП. Часто этот параметр задают разработчику АЦП.
Рассмотрим более подробно место АЦП при выполнении операции дискретизации.
Для достаточно узкополосных сигналов операцию дискретизации можно выполнять с помощью самих АЦП и совмещать таким образом с операцией квантования. Основной закономерностью такой дискретизации является то, что за счет конечного времени одного преобразования и неопределенности момента его окончания, зависящего в общем случае от параметров входного сигнала, не удается получить однозначного соответствия между значениями отсчетов и моментами времени, к которым их следует отнести. В результате при работе с изменяющимися во времени сигналами возникают специфические погрешности, динамические по своей природе, для оценки которых вводят понятие апертурной неопределенности, характеризующейся обычно апертурным временем.
Апертурным временем ta называют время, в течение которого сохраняется неопределенность между значением выборки и временем, к которому она относится. Эффект апертурной неопределенности проявляется либо как погрешность мгновенного значения сигнала при заданных моментах измерения, либо как погрешность момента времени, в который производится измерение при заданном мгновенном значении сигнала. При равномерной дискретизации следствием апертурной неопределенности является возникновение амплитудных погрешностей, которые называются апертурными и численно равны приращению сигнала в течение апертурного времени.
Если использовать другую интерпретацию эффекта апертурной неопределенности, то ее наличие приводит к "дрожанию" истинных моментов времени, в которые берутся отсчеты сигнала, по отношению к равноотстоящим на оси времени моментам. В результате вместо равномерной дискретизации со строго постоянным периодом осуществляется дискретизация с флюктуирующим периодом повторения, что приводит к нарушению условий теоремы отсчетов и появлению уже рассмотренных апертурных погрешностей в системах цифровой обработки информации.
Такое значение апертурной погрешности можно определить, разложив выражение для исходного сигнала в ряд Тейлора в окрестностях точек отсчета, которое для j-й точки имеет вид
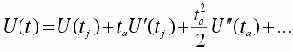
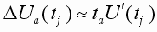 |
(4) |
Обычно для оценки апертурных погрешностей используют синусоидальный испытательный сигнал U(t)=Umsinwt, для которого максимальное относительное значение апертурной погрешности
